Un peu d’analyse et de traitement de l’image

02 mars 2023

Analyse image

Tech

Traitement image

Introduction

Dans le cadre du programme Auto, DARVA travaille à la mise en place d’une solution mobile de captation par l’assuré des photos des dommages de son véhicule sinistré. Lorsque l’assuré souhaite déclarer un sinistre, il crée en premier lieu son dossier. Un sms lui est alors envoyé afin de prendre des photos de son véhicule selon un ordre précis tout autour de la voiture. Ces images sont alors transmises au réparateur qui donne un retour sur son expertise. Cependant, pour éviter des photos de mauvaise qualité (floues ou mal contrastées) ou bien, mal cadrées, il est donc intéressant d’analyser automatiquement les images dès leurs captures pour éviter des délais supplémentaires.

On part du principe que les photos de voitures qui seront envoyées seront toutes cadrées à peu près correctement. Celle-ci étant immobile et au centre de l’image.

Configuration

La suite du billet présentant des résultats et leurs temps d’exécution, voici la configuration de la machine sur lesquelles les algorithmes ont été testés ainsi que les versions des technologies utilisées :

Processeur	11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz
Mémoire	16,0 Go, 3200MHz, SODIMM
Carte graphique	NVIDIA T600 Laptop GPU

De plus, toutes les images de voitures utilisées proviennent de la même banque de données présentes sur Kaggle.

Python 3.10

Version 4.6

Pour commencer

Avant toutes choses, ce billet va contenir quelques formules mathématiques mais pas de panique, elles ne sont là qu’à titre informatif.

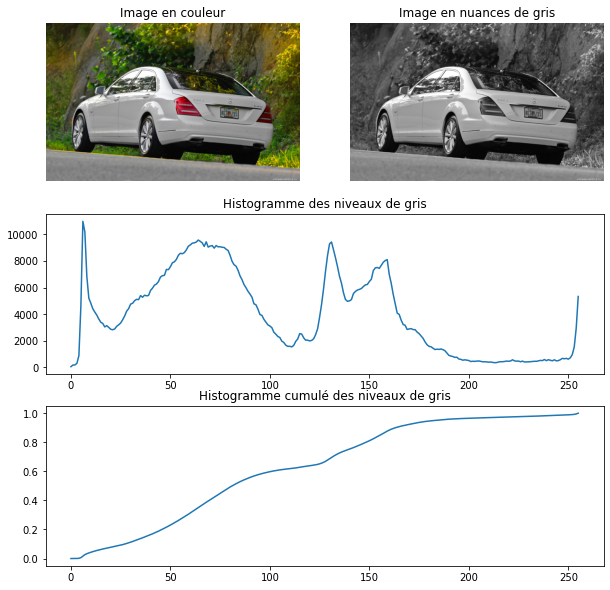
On commence donc par définir c’est qu’est une image de taille $N \times M$ en couleurs et en nuances de gris :

$f : ([0, N[, [0, M[) \to [0,255]^3$ Pour une image RGB (Rouge Vert Bleu)

$g : ([0, N[, [0, M[) \to [0,255]$ Pour une image en nuances de gris

On a donc $f(x,y)$ qui correspond à la valeur du pixel aux coordonnées $(x,y)$ avec $x \in [0, N[$ et $y \in [0, M[$

Une image en niveaux de gris étant définie par :

$g(x,y) = f(x,y). \begin{bmatrix}0.299 & 0.587 & 0.114 \end{bmatrix}^T$

Où $M^T$ correspond à la transposée de la matrice $M$ . Les coefficients, eux, correspondent aux pondérations de chaque canaux. L’œil humain étant plus sensible à la couleur verte, son coefficient est alors plus élevé. Ainsi :

$g(x,y) = R \times 0.299 + G \times 0.587 + B \times 0.114$

L’histogramme d’une image correspond à la distribution des niveaux de gris dans l’image. Et qui correspond à la probabilité d’occurrence d’un niveau de gris.

$H(i) = Card(\{ x \in [0,N[, y \in [0,M[ \ | \ f(x,y) = i\})$

Où $Card(E)$ correspond à la cardinalité (nombres d’éléments) de l’ensemble E

L’histogramme cumulé correspond lui à la somme partielle des niveaux de gris :

$H_c(i) = \sum_{j=0}^{i} H(j)$

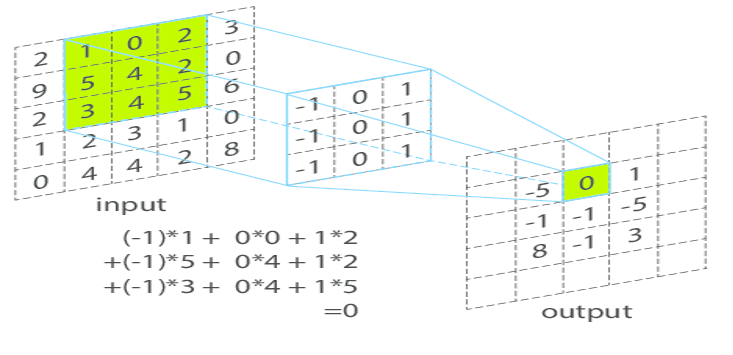Convolution d’une image (input) par un noyau (3×3).
Image disponible par Benjamin Perret

La variance d’une image en niveaux de gris est définie comme suit :

$Var(f(x,y)) = \frac{\sum_{i=0}^{N-1}\sum_{j=0}^{M-1} (f(i,j) - \overline{f})^2}{N \times M}$

Où $\overline{f}$ est la moyenne des niveaux de gris de l’image définie par :

$\overline{f} = \frac{\sum_{i=0}^{N-1}\sum_{j=0}^{M-1} f(i,j)}{N \times M}$

La convolution d’une image $f$ aux points $(x,y)$ avec un noyau $k$ de taille $2a \times 2b$ est définie par :

$\begin{align*}c(x,y) &= k * f(x,y) \\&= \sum_{dx=-a}^{a}\sum_{dy=-b}^{b}k(dx,dy)f(x - dx, y - dy)\end{align*}$

Prétraitement des images

Dans le contexte de Flash, les images envoyées ont toutes la même dimension ( $800 \times 600$ pixels). Elles sont au préalable redimensionnées du côté client en gardant les proportions. Cette technique entraîne par conséquent l’ajout de bandes noires sur les bords de l’image. Il est nécessaire de les enlever pour ne pas influencer les calculs des propriétés de l’image.

Les images étant reçues en format RGB (3 octets par pixel) on commence par la convertir en niveaux de gris (1 octet par pixel). On applique ensuite un seuillage sur l’image afin d’extraire les bordures.

$s(x,y) = \left\{\begin{matrix}255 & \text{si } g(x,y) > 0 \\0 & \text{sinon}\end{matrix}\right.$

où $s(x,y)$ est l’image en niveau de gris seuillée.

On calcule ensuite le rectangle englobant les pixels supérieurs à 0 et on rogne l’image suivant ce rectangle.

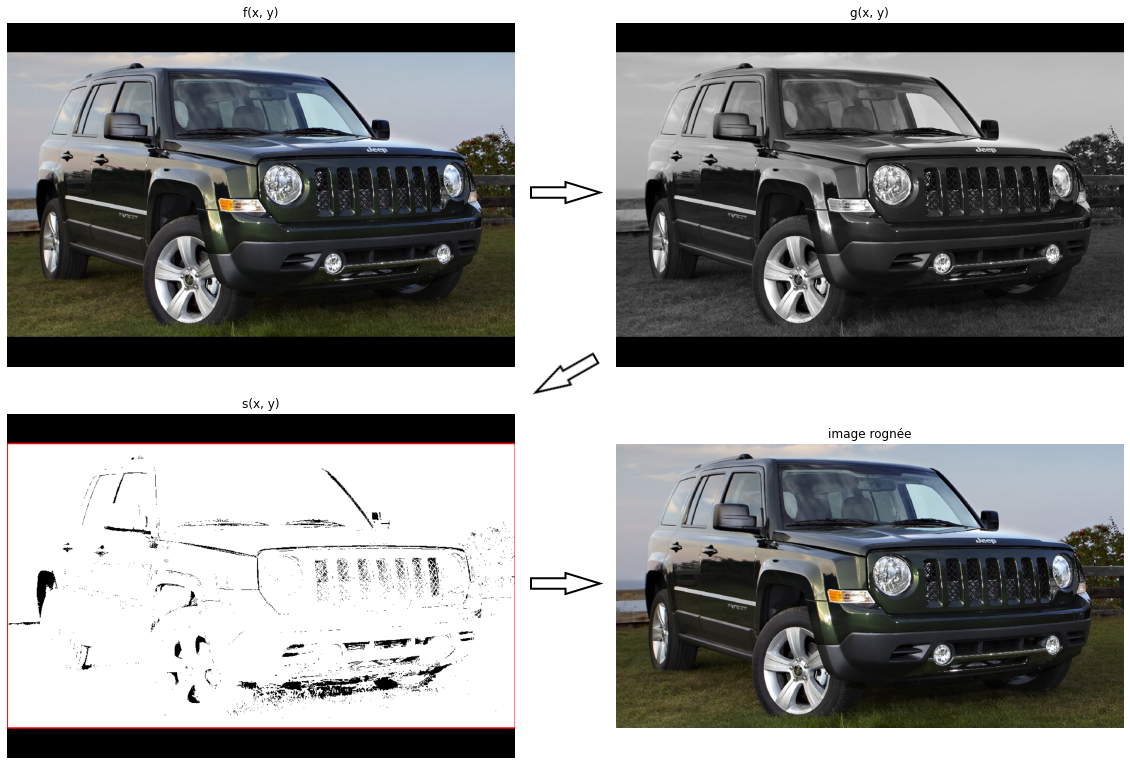Seuillage et rognage (suppression des bandes noires latérales)

Détection de flou

Pour détecter si l’image est floue, il faut d’abord calculer un score que l’on pourra ensuite comparer à un seuil. Ici, les trois méthodes que nous allons étudier se basent toutes sur la détection des contours de l’image (d’où le prétraitement des images). Plus il y a de contours détectés, moins l’image a de chances d’être floue, et inversement, plus l’image est floue, moins les contours sont détectables. Cette technique est assez fiable et les photos de voitures offrant un grand nombre de contours, cela nous permet une plus grande précision des calculs.

Les portables d’aujourd’hui adaptant le focus assez précisément, on sera plus enclin à recevoir une image contenant un flou de mouvement.

(A gauche) Flou de mouvement horizontal. (A droite) Flou lié au focus (flou Gaussien)

Variance du filtre de Laplace

La première méthode étudiée consiste à convoluer (filtrer) l’image source par le filtre de Laplace puis d’en calculer la variance. Un résultat élevé indique de grandes variations dans l’image. Plus une image possède des contours, plus cette variation est grande. Elle aura donc moins de chances d’être considérée comme floue.

$Var(f_{lapl}(x,y)) = Var\left(\begin{bmatrix}0 & -1 & 0 \\-1 & 4 & -1 \\0 & -1 & 0 \end{bmatrix} * f(x,y) \right)$

Où la matrice correspond au filtre Laplacien et * correspond à l’opérateur de convolution. On obtient donc les résultats suivants :

Calcul de la variance du filtre de Laplace sur une image nette et une image floue

Une fois la variance récupérée, on la compare à une valeur que l’on fixe comme étant le minimum acceptable pour que l’image ne soit pas considérée comme floue. Après tests, les résultats sont les suivants :

Seuil appliqué	Taux d’erreur	Temps d’exécution moyen
215	3.42%	0.04s

Moyenne des fréquences de l’image

La deuxième méthode consiste à récupérer les fréquences de l’image par une transformée de Fourier puis d’en faire la moyenne. Plus une image contient de hautes fréquences, plus elle possède des contours, et à l’inverse, plus il y a de basses fréquences, moins l’image en possède.

Le domaine fréquentiel d’une image correspond à la variation de l’intensité sur une certaine distance par rapport à un point. Il est possible de le calculer en utilisant la Transformée de Fourier discrète définie par :

$F(x,y) =\sum_{m=0}^{M-1}\sum_{n=0}^{N-1} f(m,n) e^{-i2\pi \left (\frac{xm}{M} +\frac{yn}{N} \right )}$

Où $f(x,y)$ est une image en niveaux de gris, $F(x,y)$ sa transformée de Fourier et $i$ est le nombre imaginaire.

Le résultat étant complexe, on calcule son module (la valeur absolue) pour avoir un nombre réel et calculer la moyenne plus facilement.

$|x + iy| = \sqrt{x^2 + y^2}$

Calcul de la moyenne des spectres par transformée de Fourier discrète

On constate alors une moyenne bien plus faible dans le spectre de l’image floue que dans celle de l’image nette. On compare ensuite cette valeur à un seuil. On obtient alors les résultats suivants :

Seuil appliqué	Taux d’erreur	Temps d’exécution moyen
5250	1.08%	0.11s

Variance du filtre de Sobel

Cette méthode fonctionne de la même façon que la variance du filtre de Laplace, la seule différence se trouvant au niveau du filtre ainsi que du nombre d’opérations. Au lieu d’appliquer un seul filtre, on va en appliquer trois différents pour calculer les contours sur l’horizontale, la verticale et la diagonale. Ainsi les différents résultats sont respectivement définis par :

$G_x(x,y) = \left(\begin{bmatrix}-1 & 0 & 1 \\-2 & 0 & 2 \\-1 & 0 & 1 \\\end{bmatrix} * f(x,y) \right)$

$G_y(x,y) = \left(\begin{bmatrix}-1 & -2 & -1 \\0 & 0 & 0 \\1 & 2 & 1 \\\end{bmatrix} * f(x,y) \right)$

$G_{xy}(x,y) = \left(\begin{bmatrix}1 & 0 & -1 \\0 & 0 & 0 \\ -1 & 0 & 1 \end{bmatrix} * f(x,y)\right)$

On calcule ensuite la variance de chaque gradient

$\\Var_x = Var(G_x(x,y)) \\Var_y = Var(G_y(x,y)) \\Var_{xy} = Var(G_{xy}(x,y))$

Calcul de la variance de chaque gradient produit par les filtres de Sobel

L’avantage de cette technique par rapport aux autres est qu’elle nous permet de comparer l’image sur trois valeurs différentes et donc d’affiner les résultats.

Le fait de détecter les variations sur l’horizontale, la verticale et la diagonale nous permet de mieux détecter le flou de mouvement. Par exemple, si une image a un flou de mouvement horizontal, la valeur de $G_x(x,y)$ sera élevée et celle de $G_y(x,y)$ sera faible.

Seuil appliqué	Taux d’erreur	Temps d’exécution moyen
x : 1200, y : 2650, xy : 80	0.94%	0.15s

Conclusion sur la détection de flou

Méthode	Taux d’erreur	Temps d’exécution moyen
Variance Laplace	3.42%	0.04s
Moyenne des fréquences	1.08%	0.11s
Variance Sobel	0.94%	0.15s

On constate que la solution proposant les meilleurs résultats est la variance du filtre de Sobel. Cependant, celle-ci est la plus gourmande en temps de calcul (ce qui est dû aux trois convolutions, on remarque d’ailleurs que $T_{sobel} \simeq 3 \times T_{laplace}$ ). Toutefois, la variance du filtre de Sobel peut être parallélisée assez simplement ce qui permettrait d’abaisser le temps de calcul.

Analyse du contraste

En plus du flou, une image peut être mal contrastée. La première question qu’on est en droit de se poser est : « Mais c’est quoi une image mal contrastée ? ». Eh bien dans notre cas, c’est une image qui a peu de variations de niveaux de gris (ou de couleurs) comparées à la taille de l’image. On compte aussi en tant que mauvais contraste, les images prises en contre jour qui, elles, sont très contrastées (une partie très claire et une partie très foncée). Les prochaines techniques se basent en grande partie sur l’histogramme et l’histogramme cumulé (définis dans le préambule) qui est un bon indicateur du contraste d’une image.

Écart-type de l’image en niveau de gris

La première technique consiste à calculer l’écart-type des niveaux de gris de l’image. On va comparer les résultats à une valeur de seuil inférieur et supérieur. Cette technique se nomme « le contraste RMS » pour « Root Mean Square ». Comme l’écart-type est égal à la racine carrée de la variance, on le calcule comme suit :

$RMS = \sqrt{Var(g(x,y))}$
Calcul du contraste RMS sur l’image préalablement convertit en niveaux de gris

Seuils appliqués	Taux d’erreur	Temps d’exécution moyen
inférieur : 45, supérieur : 75	25.02%	0.06s

Étalement d’histogramme

L’étalement d’histogramme ou l’Histogram Spread (HS), consiste à calculer le ratio de la distance du niveau de gris entre 25% et 75% de la valeur maximale.

$HS = \frac{Q_3(H_c) - Q_1(H_c)}{max - min}$

Avec $max$ et $min$ étant les valeurs maximales et minimales de la plage de calcul (ici 255 et 0). $Q_1$ et $Q_3$ étant respectivement les antécédents de 25% et 75% de l’histogramme cumulé.

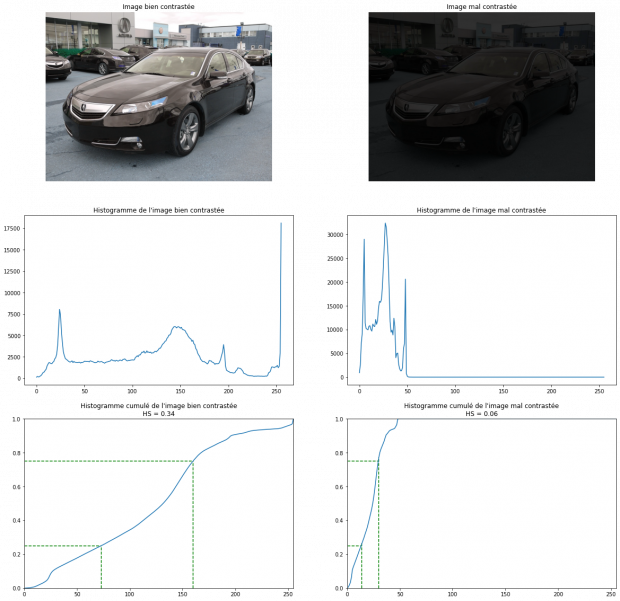Calcul de l’étalement d’histogramme sur l’histogramme cumulé. Les lignes vertes correspondant à Q1 et Q3

Seuils appliqués	Taux d’erreur	Temps d’exécution moyen
inférieur : 0.27, supérieur : 0.6	26.45%	0.30s

Corrélation d’histogrammes cumulés

Une image peut être considérée comme parfaitement contrastée si la valeur des ses pixels est répartie uniformément sur tout son histogramme $y = \frac{\text{nb pixels}}{256}$ . Son histogramme cumulé sera alors de la forme $y = \frac{\text{nb pixels}}{256}x$ .

La corrélation de nos deux histogrammes va nous donner un bon paramètre sur leurs ressemblances. Ainsi, si l’histogramme cumulé de l’image se rapproche de celui de l’histogramme cumulé considéré parfait, elle aura plus de chances d’être idéalement contrastée.

$Corr_k = \sum _n H(n+k).\overline{H_c(n)}$

Où $\overline{H_c(n)}$ est le conjugué de $H_c(n)$

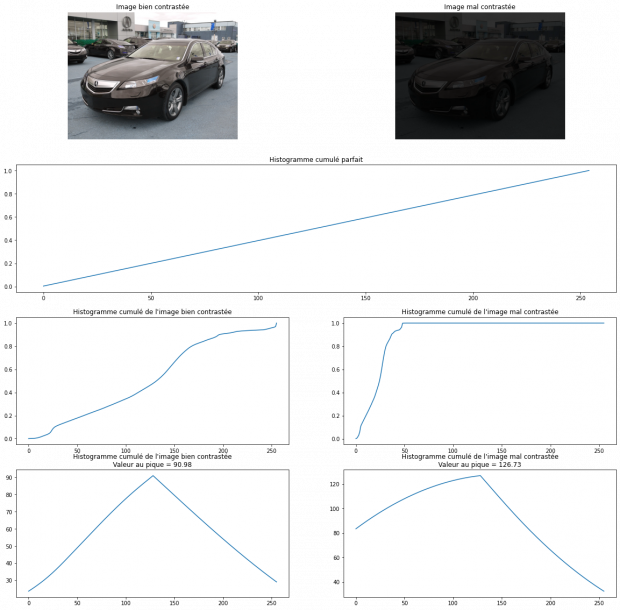Calcul de la corrélation entre les histogrammes cumulés des images et l’histogramme cumulé parfait

Seuils appliqués	Taux d’erreur	Temps d’exécution moyen
inférieur : 72, supérieur : 119.5	7.40%	1.24s

Écart-type sur des portions d’histogramme

Cette technique consiste à séparer l’histogramme cumulé en dix parties sur lesquelles nous allons calculer le ratio de la distance entre la borne inférieure et supérieure et la distance totale de l’histogramme cumulé. Plus l’écart-type sera élevé, plus il y aura une chance d’avoir un pic dans l’histogramme.

$P(i) = D_i(H_c) - D_{i-1}(H_c)$

Avec $D_i$ étant le i-ème décile, $H_c$ l’histogramme cumulé et $i \in ]0, 10[$

On récupère ensuite l’écart-type de $P$ :

$\sigma(P) = \sqrt{\frac{1}{10}\sum_i(P(i) - \overline{P})^2}$

Où $\overline{P}$ correspond à la moyenne de $P$

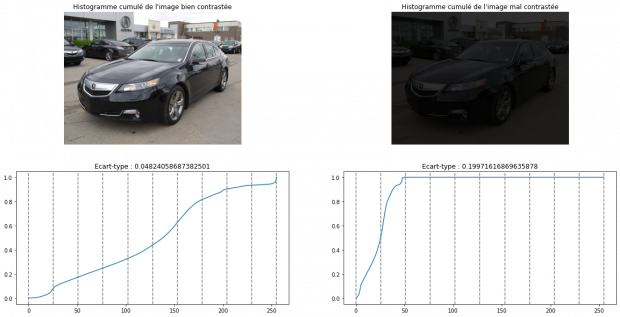Calcul de l’écart-type entre les dix distances calculées dans chaque portion

Seuil appliqué	Taux d’erreur	Temps d’exécution moyen
0.1115	6.76%	1.15s

Conclusion sur l’analyse du contraste

Méthode	Taux d’erreur	Temps d’exécution moyen
RMS	25.02%	0.06s
HS	26.45%	0.30s
Corrélation	7.40%	1.24s
Écart-type sur portions	6.76%	1.15s

On constate deux parties dans les résultats, la première avec les méthodes RMS et HS ayant un taux d’erreur plutôt élevé mais rapide à l’exécution et les deux autres méthodes ayant un faible taux d’erreur mais un temps d’exécution supérieur à 1s. Pour l’instant, la technique la plus prometteuse se trouve être le calcul de l’écart-type sur les portions d’histogramme. De plus, cette méthode permet de détecter les images prises en contre-jour car la présence de deux pics dans l’histogramme augmentera l’écart-type.

Il faut aussi savoir que corriger une image mal contrastée est assez simple. Il nous suffit d’appliquer une égalisation d’histogramme. Si l’image est mal contrastée, l’opération va alors répartir les valeurs des pixels de la manière la plus équitable dans l’histogramme. Si l’image était de base bien contrastée, alors l’égalisation ne détériore pas trop l’image.

Il peut donc être intéressant de comparer l’application d’une des méthode d’analyse de la première partie (RMS ou HS) en la faisant suivre d’une égalisation aux méthodes de la deuxième partie. Alors, même si l’image sera considérée comme mal contrastée (une image sur quatre dans ce cas), l’amélioration ne changera pas l’image et le temps de calcul restera inférieur au temps de calcul des méthodes de la deuxième partie.

Pour finir

Il existe aujourd’hui encore d’autres façons de détecter du flou ou d’analyser le contraste d’une image. Les techniques dépendent surtout du contexte dans lequel on se trouve. Il en va de même pour les seuils que nous avons utilisés pour classer les images.

Une des approches qui aurait tendance à être plus efficace serait l’apprentissage d’un réseau de neurones qui calibre lui-même les seuils de manière plus précise. Bref, l’analyse et le traitement de l’image a encore beaucoup à donner dans le monde de l’assurance (on aura l’occasion de le voir dans un autre billet, ne vous inquiétez pas). En plus de la détection de détériorations de l’image, il peut être intéressant de reconnaître ce qui est pris en photo, de détecter la plaque d’immatriculation (petit spoiler) et bien d’autres choses encore. Toute cette présentation a d’ailleurs été réalisée sur la partie assurance auto mais elle peut tout aussi bien s’appliquer pour de l’assurance habitation.

Comme vous avez pu le comprendre, cette preuve de concept n’est qu’une petite brique de l’analyse et du traitement de l’image au service de la gestion des sinistres et des assurances.

Ce sujet à propos de l’analyse et au traitement d’image vous a intéressé ? Sur le même thème, découvrez le nouveau billet de Vincent consacré à la lecture automatisée d’une carte-grise.

À propos de l'auteur.
Vincent Commin est Alternant au sein du DARVALab et 
en Master 2 Conception Logicielle à l'université de Poitiers.
Passionné par la recherche, le développement et l'intégration 
de nouvelles solutions et technologies au service des
développeurs et des utilisateurs.